Unlike traditional CFD solvers which numerically solve a set of partial different equations, e.g. Navier-Stokes equations, for fluid flows at macroscopic level, Polaris CFD's core solver starts with the Boltzmann equations, which is more fundamental and general for describing fluid particle motions at microscopic levels. A Navier-Stokes solver can be recovered theoretically by solving the Boltzmann equations. In a Gas Kinetic representation, a single particle distribution function is calculated in continuous particle velocity space, and all macroscopic flow variables, such as mass, momentum and energy, are moments of the single particle distribution function.

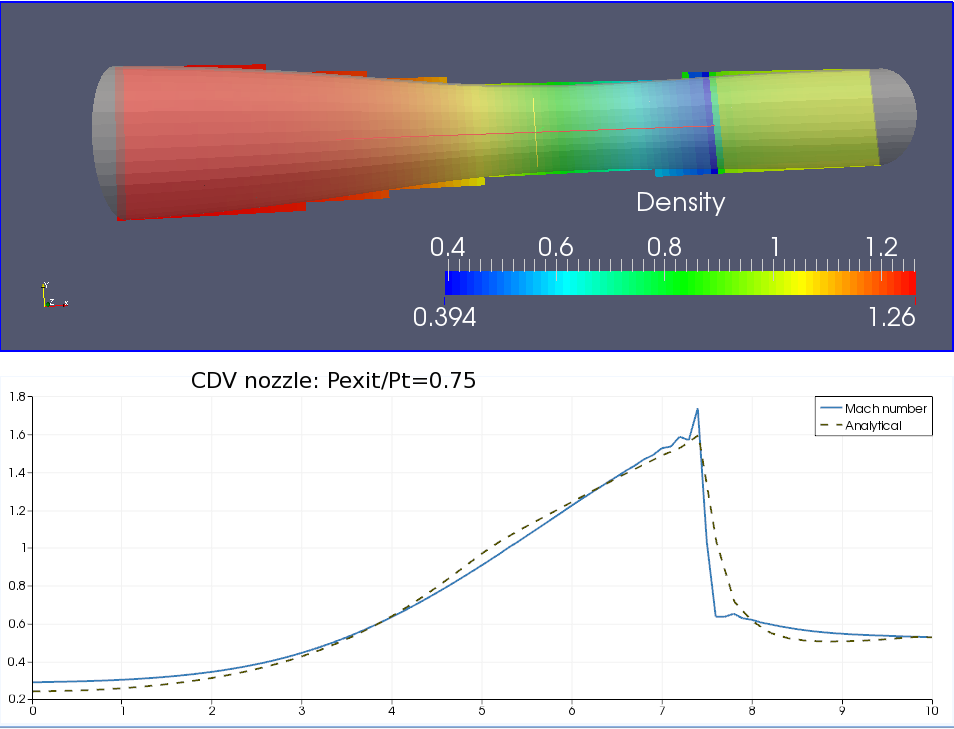
In Polaris CFD, the Gas Kinetic approach is realized on a structured cartesian mesh. The single particle distribution function is calculated explicitly on discrete cell interface by applying the general Boltzmann solution. The fluid flow fluxes across the cell interface, including fluxes of mass, momentum and energy are determined by measuring the moments of the local particle distribution function. Since there is explicit calculation of flow advection and diffusion, the fluxes of fluid flow can be computed accurately and conservation law can be satisfied easily. As a result the numerical scheme is simpler than traditional CFD solvers. Polaris is especially suitable for compressible flow simulations ranging from subsonic to supersonic regime. No special shock capture technique is required. Because all the Gas Kinetic computations are local, this approach is rather ideal for parallel computation on massive clusters.

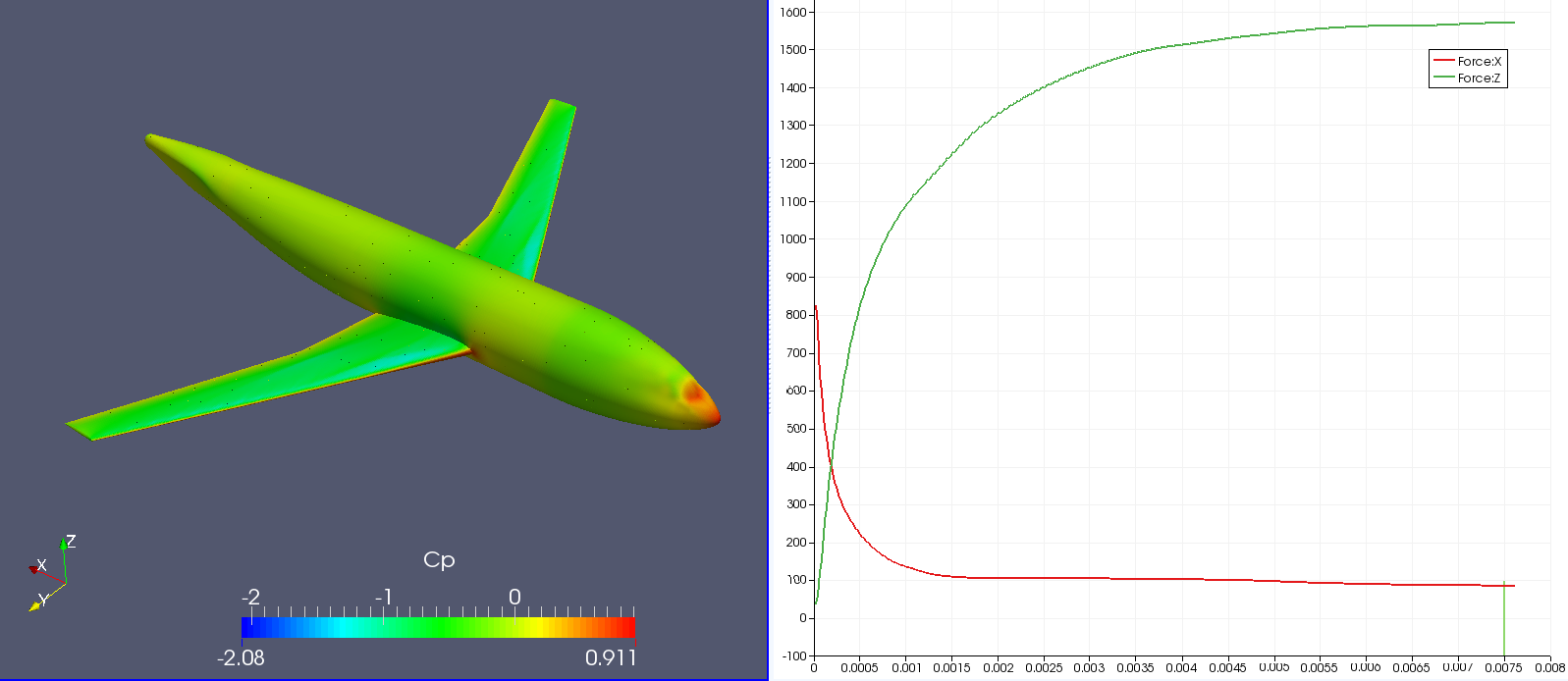
Polaris has developed a generalized Gas Kinetic boundary condition on arbitrary geometries. In Polaris CFD solver, complex geometries are discretized into piecewise linear planary facets in two dimensions or polygons in three dimensions. By taking advantage of its kinetic nature, both a noslip boundary condition and a frictionless boundary condition can be realized precisely with exact conservation law obeyed. For both boundary conditions, mass flux conservation is realized. Surface tangential momentum flux conservation is also achieved in frictionless boundary condition, which is critical for modeling turbulent boundary layer.

Because of the limitation of current computational power, turbulence modeling is necessary for solving sub-grid scale fluid flow motions in real applications. Polaris offers two types of turbulence models, standard k-e RNG two equations model and Large Eddy Simulation (LES) model. Within the LES model, users could have two options, one with the standard Smagorinsky model and the other with Wall-Adapting local eddy-viscosity (WALE) model. These turbulence models have been well studied and extensively used in general CFD community. Since there is no universal turbulence model for general fluid flows, users could have freedom in Polaris to make the best choice for their own problems. Instead of fully resolving turbulent boundary layer which requires extremely fine local resolutions, a turbulent wall function is applied in Polaris to give an accurate estimation of local turbulent momentum flux. Together with the generalized wall boundary condition described in the previous section, turbulent boundary layer can be appropriately simulated then.